1.8 Μέθοδοι

Διαίρει και βασίλευε

Για να αντιμετωπιστούν πολύπλοκα προβλήματα, ένας καλός τρόπος είναι ο μοιρασμός τους («σπάσιμο») σε μικρότερα. Άλλος λόγος είναι η αποφυγή επαναλαμβανόμενου κώδικα. Αν επαναλαμβάνουμε τμήματα κώδικα πολλές φορές, τότε αν χρειαστεί ν’ αλλάξουμε αυτό το τμήμα κώδικα, θα πρέπει να το κάνουμε σε όλα τα αντίγραφα.

Αξίωμα: «Μην Επαναλαμβάνεσαι» (DRY – Don’t Repeat Yourself)

Στη Java αυτό το πετυχαίνουμε τμηματοποιώντας τον κώδικα σε μεθόδους.

Μια μέθοδος ορίζεται ως εξής:

τύπος_επιστροφής όνομα_μεθόδου(παράμετροι);

Π.χ.

jshell> double perimeter(double r) {  // y = perimeter(r)
           return 2*Math.PI*r;
        }
| created method perimeter(double)
jshell> int x = 10
x ==> 10
jshell> perimeter(x)
$3 ==> 62.83185307179586
jshell> /methods
|    perimeter (double)double

Παραπάνω ορίσαμε μια μέθοδο perimeter() η οποία λαμβάνει ως όρισμα (παράμετρο) έναν double και επιστρέφει έναν double. Μια μέθοδος είναι σαν μια συνάρτηση στα μαθηματικά, π.χ. y = f(x). Δέχεται ένα όρισμα x και επιστρέφει μια τιμή y.

jshell> void myPrint(String... lines) {  // varargs
           for (String e : lines) {
		       System.out.println(e);
           }
        }    
|  created method myPrint(String...)
jshell> String[] sentences = new String[] {
"Καλήν εσπέραν άρχοντες",
"πώς είναι ο ορισμός σας"
};
sentences ==> String[2] { "Καλήν εσπέραν άρχοντες", ... }
jshell> myPrint(sentences)
Καλήν εσπέραν άρχοντες
πώς είναι ο ορισμός σας

Η σύνταξη String... είναι ισοδύναμη με String[] και ονομάζεται vararg. Πρέπει να είναι η τελευταία παράμετρος μιας μεθόδου.

Πέρασμα Παραμέτρων δια τιμής (By value) και δια αναφοράς (by reference)

Όταν καλέσαμε την μέθοδο perimeter(x) παιρνώντας της την παράμετρο x, αυτό που συμβαίνει πίσω από τη σκηνή είναι ότι το όρισμα r παίρνει την τιμή της παραμέτρου x (δηλ. την τιμή 10) που χρησιμοποιείται στους υπολογισμούς της περιμέτρου. Αυτό καλείται πέρασμα παραμέτρων με τιμή (by value) καθώς η τιμή της παραμέτρου κλήσης x αντιγράφεται στο όρισμα r. Αν αλλάξουμε την τιμή της r, η τιμή της x δεν αλλάζει, καθώς μόνο η τιμή της αντιγράφηκε στην r. Αυτό ισχύει κατά κανόνα όταν τα ορίσματα είναι πρωτογενείς τύποι.

jshell> void changeParameter(int i) {
   ...>    i = 10;
   ...> }
|  created method changeParameter(int)

jshell> int a = 3
a ==> 3

jshell> changeParameter(a)

jshell> a
a ==> 3

Στο παραπάνω παράδειγμα δημιουργήσαμε μια μέθοδο changeParameter() η οποία δέχεται ένα όρισμα τύπου int και το αλλάζει στο σώμα της μεθόδου (αλλάζει την τιμή του σε 10). Στη συνέχεια καλούμε αυτή τη μέθοδο παιρνώντας της την μεταβλητή a την οποία έχουμε αρχικοποιήσει στην τιμή 3. Ενώ περιμένουμε η μέθοδος ν’ αλλάξει την τιμή της μεταβλητής a σε 10, αυτό δε συμβαίνει, και η τιμή της a παραμένει 3. Όπως εξηγήσαμε πιο πάνω, επειδή ο int είναι πρωτογενής τύπος (raw type) δημιουργείται ένα αντίγραφο της τιμής της a και το αντίγραφο αυτό είναι που τροποποιείται μέσα στο σώμα της μεθόδου, αφήνοντας την τιμή της αρχικής μεταβλητής a ανέπαφη.

Όταν τα ορίσματα των μεθόδων είναι όμως τύποι κλάσεων (όπως θα δούμε στα μαθήματα της επόμενης εβδομάδας) ή πίνακες (arrays) τότε δεν αντιγράφεται η τιμή τους, αλλά αντιγράφεται η διεύθυνση μνήμης του αντικειμένου/πίνακα στην μεταβλητή του ορίσματος, γι’ αυτό κι αυτή η περίπτωση ονομάζεται πέρασμα παραμέτρων με αναφορά (by reference). Έτσι στο ακόλουθο παράδειγμα, το όρισμα array αναφέρεται στη θέση μνήμης που δείχνει ο πίνακας a. Αυτό σημαίνει ότι ο κώδικας της μεθόδου printArray() τροποποιώντας το 1ο στοιχείο του ορίσματος array, τροποποιεί τα δεδομένα του πίνακα a, αφού η array δείχνει στην ίδια θέση μνήμης με την a. Γι’ αυτό το λόγο θέλει μεγάλη προσοχή όταν αλλάζουμε τις τιμές των ορισμάτων όταν αυτά είναι αντικείμενα/συστοιχίες. Θα δούμε ακόμα ένα παράδειγμα στα μαθήματα της επόμενης εβδομάδας όταν θα μιλήσουμε για κλάσεις και αντικείμενα κλάσεων.

jshell> void printArray(int[] array) {
   ...>     array[0]=100;
   ...>     for (int i=0; i<array.length; i++) {
   ...>         System.out.print(array[i] + ", ");
   ...>     }
   ...>     System.out.println();
   ...> }
|  created method printArray(int[])

jshell> int[] a = {1, 2, 3, 4, 5};
a ==> int[5] { 1, 2, 3, 4, 5 }

jshell> printArray(a)
100, 2, 3, 4, 5, 

jshell> a
a ==> int[5] { 100, 2, 3, 4, 5 }

Εμβέλεια μεταβλητών

Οι μεταβλητές είναι ορατές μόνο στο μπλοκ που ορίζονται μέσα σε { } και σε εμφωλιασμένα μπλοκ.

{                                     __
   int x;                               |
   {                           __       |
	int y;                  | y    | x
   }                           __       |
   ...  // η y δεν υπάρχει              |
}                                      __

void printTree(int treeWidth) {
   int i;                                              __
   for (i = 1; i < treeWidth; i = i + 2) {               |
      int j;                                       __    |
      for (j = 0; j < (treeWidth - i) / 2; j++)	     |   |
         System.out.print(' ');                      |   |
      for (j = 0; j < i; j++)                        |   |
         System.out.print('*');	                     |   |
      System.out.println();                          |   |
   }                                                __   |
}                                                       __

Υπερφόρτωση μεθόδων (method overloading)

Μπορούμε να ορίσουμε μεθόδους που έχουν το ίδιο όνομα αλλά δέχονται διαφορετικές παραμέτρους (είτε διαφορετικό αριθμό παραμέτρων είτε ίδιο αριθμό αλλά με διαφορετικούς τύπους δεδομένων).

Π.χ.

  int calculate(int x, int y) {
	  return x*y;
  }
  double calculate(double x, double y) {
  	return x*y; 
  }
  int calculate(int x, int y, int z) {
	  return x*y*z;
  }
}

Λέμε ότι η μέθοδος calculate() έχει υπερφορτωθεί.

Σημειώστε ότι είναι λάθος μεταγλώττισης να ορίσετε δυο μεθόδους με το ίδιο όνομα και αριθμό και τύπο παραμέτρων που να επιστρέφουν όμως διαφορετικό τύπο δεδομένων. Η υπερφόρτωση αφορά μόνο τον τύπο και τον αριθμό των παραμέτρων.

  int calculate(double x, double y) {
	  return (int)(x*y);
  }
  double calculate(double x, double y) {
  	return x*y; 
  }

Οι παραπάνω δηλώσεις προκαλούν λάθος μεταγλώττισης.

Αναδρομή

Μια μέθοδος ονομάζεται αναδρομική όταν καλεί τον εαυτό της.

// υπολογισμός του n παραγοντικό
jshell> int factorial(int n) {
	     if (n <= 1) {
        	return 1;
	     } else {
		    return n * factorial(n-1);
	     }	
        }
|  created method factorial(int)
jshell> factorial(3)
$4 ==> 6

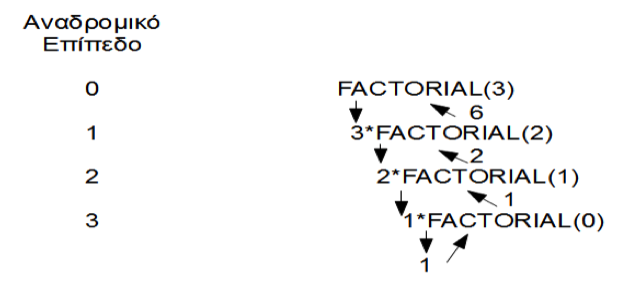
Εικόνα 1.8.1 Υπολογισμός παραγοντικού αναδρομικά

Η factorial() καλεί τη factorial() μέσα στο σώμα της. Μια αναδρομική μέθοδος θα πρέπει να έχει μια συνθήκη τερματισμού διαφορετικά δε θα τερματίσει ποτέ. Η factorial() διαθέτει τη συνθήκη if (n <= 1) που πρέπει να κληθεί τελικά.

Ασκήσεις

Να γράψετε δυο μεθόδους που θα δέχονται ως παραμέτρους την ακτίνα σφαίρας και θα υπολογίζουν η μία την επιφάνεια και η άλλη τον όγκο της σφαίρας. (Χρήσιμος υπερσύνδεσμος).
Να γράψετε μια μέθοδο που μετράει τα κεφαλαία και πεζά γράμματα σε μια φράση που περνιέται σ’ αυτήν ως παράμετρος. (Στην επίλυση του βίντεο δεν μετρώνται τα τονούμενα πεζά γράμματα. Τροποποιήστε τη λύση του βίντεο ώστε να προσμετρώνται τα πεζά και τα τονούμενα γράμματα).
Να γράψετε μια μέθοδο που λαμβάνει ως παράμετρο έναν πίνακα από αριθμούς ή ένα vararg και επιστρέφει έναν πίνακα με τα μοναδικά στοιχεία του αρχικού.
Να γράψετε μέθοδο initials(String text) που δέχεται ως είσοδο ένα κείμενο και επιστρέφει το κείμενο με το αρχικό μόνο σύμβολο κάθε λέξης του (π.χ. αν text = "Καλημέρα σας", επιστρέφει "Κ. Σ.").
Να υλοποιήσετε στη Java το κόσκινο του Ερατοσθένη για να υπολογίσετε όλους τους πρώτους αριθμούς μέχρι έναν συγκεκριμένο ακέραιο n (int[] Eratosthenis(int n)) όπως περιγράφεται στη Βικιπέδια.
Επαναλάβετε την άσκηση 2 (Αλγόριθμος κρυπτογράφησης του Καίσαρα) του 4ου μαθήματος γράφοντας δυο γενικές μεθόδους String encrypt(String plainText, int key) και String decrypt(String encryptedText, int key) που θα κωδικοποιούν και θα αποκωδικοποιούν ένα αλφαριθμητικό που περνιέται ως παράμετρος σύμφωνα με τον αλγόριθμο κρυπτογράφησης του Καίσαρα.
Να γραφτεί μια μέθοδος boolean anagram(String s1, String s2) που θα δέχεται δυο συμβολοσειρές και επιστρέφει true αν η μία είναι αναγραμματισμός της άλλης. Π.χ. η λέξη φάρος είναι αναγραμματισμός της λέξης αφρός.
Μια συμβολοσειρά ονομάζεται παλινδρομική (palidrome) αν διαβάζεται το ίδιο και από τα δεξιά και από τ’ αριστερά (π.χ. η λέξη radar). Να γράψετε μια μέθοδο boolean palidrome(String s) που να διαβάζει μια συμβολοσειρά και να εξετάζει αν είναι παλιδρομική ή όχι.
Να γράψετε μια αναδρομική μέθοδο long sum(int n) που θα υπολογίζει το άθροιμα 1+2+...+n.
Να γράψετε μια αναδρομική μέθοδο που θα υπολογίζει τον αριθμό fibonacci. Ο αριθμός fibonacci ορίζεται ως: fib(n) = fib(n-1) + fib(n-2). Υπόδειξη: Υπάρχει και ένας πιο γρήγορος αναδρομικός αλγόριθμος υπολογισμού:

f(2n)=2*f(n-1)*f(n) + f(n)*f(n), αν ο n είναι ζυγός
f(2n-1)=f(n)*f(n) + f(n-1)*f(n-1), αν ο n είναι μονός

(Προσέξτε να διαιρέσετε με το 2 για να υπολογίσετε το f(n)).

11) Να γραφτεί μια αναδρομική μέθοδο που θα υπολογίζει το Μέγιστο Κοινό Διαιρέτη (ΜΚΔ) δυο φυσικών αριθμών m και n σύμφωνα με τον αλγόριθμο του Ευκλείδη:

           n              , αν n<=m και m mod n = 0  
ΜΚΔ(m,n) = ΜΚΔ(m, n)      , αν m < n
           ΜΚΔ(m, m mod n), διαφορετικά

12) Μαγικοί αριθμοί. Ο μυστήριος αριθμός 6174. Γιατί; Για να το βρείτε υλοποιήστε τον παρακάτω αλγόριθμο:

Αλγόριθμος

Γράψτε μια μέθοδο που δέχεται ως όρισμα έναν 4-ψήφιο θετικό αριθμό του οποίου όλα τα ψηφία είναι διαφορετικά, π.χ. 3546 είναι έγκυρο όρισμα (τα 3333 ή 2335 όχι).
Ταξινομήστε τα ψηφία του σε αύξουσα και φθίνουσα σειρά, π.χ. 6543 και 3456.
Αφαιρέστε τους δυο αριθμούς
Επαναλάβετε τα βήματα 2 και 3:

Π.χ. δοθέντος του 3546:

6543-3456 = 3087
8730-0378 = 8352
8532-2358 = 6174
7641-1467 = 6174 ....

Όταν σε δυο διαδοχικά βήματα λάβουμε το ίδιο αποτέλεσμα (6174) ο αλγόριθμος τερματίζεται. Σε κάθε 4-ψήφιο αριθμό (με διαφορετικά ψηφία) στον οποίο εφαρμόζεται ο παραπάνω αλγόριθμος επιστρέφει το μαγικό αριθμό 6174. Οι μαθηματικοί κατάφεραν να ελέγξουν 8891 τέτοιους 4-ψήφιους αριθμούς και έφτασαν στο αποτέλεσμα 6174 μετά το πολύ 7 αφαιρέσεις!!! Εσείς;

1.8 Μέθοδοι {#Java}

My books