3.5 Ουρές (Queues)

© Γιάννης Κωστάρας

---

<-

Δ

->

---

Η έννοια της ουράς συναντάται πολύ συχνά στην καθημερινή ζωή. Ουρές δημιουργούνται όταν άνθρωποι, εργασίες, προγράμματα κλπ. περιμένουν για να εξυπηρετηθούν. Το θέμα είναι τόσο σημαντικό και με τέτοιες πρακτικές επιπτώσεις ώστε ένας ιδιαίτερος κλάδος της Επιχειρησιακής Έρευνας, η Θεωρία Ουρών (Queueing Theory), μελετά τη συμπεριφορά και την επίδοση των ουρών. Σε μια ουρά αναμονής με ανθρώπους, εξυπηρετείται συνήθως εκείνος που στέκεται πρώτος στην ουρά. Αυτή η μέθοδος επεξεργασίας ονομάζεται Πρώτο μέσα, πρώτο έξω, ή απλούστερα FIFO (First In, First Out).

Οι εισαγωγές σε μια ουρά επιτρέπονται μόνο από το ένα άκρο ενώ οι εξαγωγές μόνο από το άλλο άκρο. Επομένως, απαιτούνται δυο δείκτες: εμπρός (front) και πίσω (rear).

Η Java παρέχει την ακόλουθη διεπαφή η οποία διαθέτει τις παρακάτω μεθόδους αλλά και άλλες που δεν εμφανίζονται:

Εικόνα 3.5.1 Η διεπαφή Ουρά της Java

public interface Queue<E> { 
   /** Insert */
   boolean offer(E e);
   /** Remove */
   E poll();
   /** Examine */
   E peek();
}

Η μέθοδος offer(E e) εισάγει ένα νέο στοιχείο στο τέλος της ουράς. Η μέθοδος E poll() εξάγει το στοιχείο από την αρχή της ουράς. Η μέθοδος E peek() επιστρέφει το στοιχείο από την αρχή της ουράς χωρίς να το αφαιρεί από την ουρά.

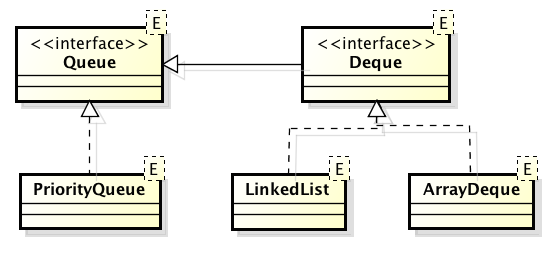
Εικόνα 3.5.2 Ουρές στη Java

Η Deque είναι μια διπλή ουρά, μπορούμε δηλ. να εισάγουμε/εξάγουμε στοιχεία από οποιοδήποτε άκρο της. Επίσης, διατηρεί τη σειρά με την οποία εισάγονται τα στοιχεία σ’ αυτήν. Αν εξάγουμε τα στοιχεία από το ίδιο άκρο από το οποίο τα εισάγαμε, τότε η Deque λειτουργεί ως Στοίβα (Stack) δηλ. Τελευταίο μέσα, πρώτο έξω, ή απλούστερα LIFO (Last In, First Out). Η ArrayDeque υλοποιείται ως ένας κυκλικός πίνακας, ενώ η LinkdedList ως συνδεδεμένη λίστα. Η τελευταία είναι η μόνη που μπορεί ν’ αποθηκεύσει null στοιχεία.

Εικόνα 3.5.3 Η διεπαφή Διπλής Ουράς της Java

Όπως βλέπουμε στην Εικόνα 3.5.3, η Deque επεκτείνει τη διεπαφή Queue με μεθόδους συμμετρικές ως προς την αρχή ή το τέλος της ουράς.

Η ουρά μπορεί να υλοποιηθεί είτε με τη βοήθεια ενός πίνακα είτε με τη βοήθεια μιας συνδεδεμένης λίστας.

jshell> Queue<Integer> q = new ArrayDeque<>();
q ==> []

jshell> Queue<Integer> q = new LinkedList<>();
q ==> []

με την πρώτη υλοποίηση να είναι πιο αποδοτική από τη δεύτερη.

public class Q<E> {
 private final Deque<E> queue;
 private final int size;
 
 public Q(int numElements) {
  this.size = numElements;
  queue = new ArrayDeque<E>(this.size);
 }
 
 // προσθήκη στο τέλος της ουράς
 public boolean push(E e) {  
  return !isFull() && queue.offer(e);
 }
 
 // αφαίρεση από την αρχή της ουράς
 public E pop() {			
   return queue.poll();
 }
 
 // προσπέλαση της αρχής της ουράς
 public E peek() {			
   return queue.peek();
 }
 
 public boolean isEmpty() {
  return queue.isEmpty();
 }
 
 public boolean isFull() {
	return queue.size() == size;
 }
}

Μια ουρά που υλοποιείται με πίνακα κινδυνεύει να γεμίσει ενώ υπάρχει ακόμα χώρος στην αρχή της, δηλ. πριν από το δείκτη εμπρός. Μια πιο αποτελεσματική υλοποίηση είναι η κυκλική ουρά (circular queue) ή δακτύλιος (ring).

Εισαγωγή στοιχείων

Χρησιμοποιήστε τη μέθοδο boolean offer(E e) για να εισάγετε ένα στοιχείο στο τέλος της ουράς. Η μέθοδος επιστρέφει true αν η εισαγωγή του στοιχείου ήταν επιτυχής, αλλοιώς επιστρέφει false. Αποφύγετε τη χρήση της boolean add(E e) από την Collection η οποία εμφανίζει IllegalStateException αν η ουρά είναι γεμάτη.

jshell> q.offer(10);
$1 ==> true

jshell> q.offer(20);
$2 ==> true

jshell> q.offer(30);
$3 ==> true

jshell> q
q ==> [10, 20, 30]

Αν χρησιμοποιείτε διπλή ουρά, τότε χρησιμοποιήστε τις μεθόδους boolean offerFirst(E e), boolean offerLast(E e) για να εισάγετε ένα στοιχείο στην αρχή ή στο τέλος της ουράς αντίστοιχα. Οι μέθοδοι επιστρέφουν true αν η εισαγωγή του στοιχείου ήταν επιτυχής, αλλοιώς επιστρέφουν false. Αποφύγετε τη χρήση των boolean addFirst(E e), boolean addLast(E e) από την Collection οι οποίες εμφανίζουν IllegalStateException αν η ουρά είναι γεμάτη.

jshell> Deque<Integer> deque = new ArrayDeque<>();
deque ==> []

jshell> deque.offerLast(10);
$4 ==> true

jshell> deque.offerLast(20);
$5 ==> true

jshell> deque.offerLast(30);
$6 ==> true

jshell> deque
deque ==> [10, 20, 30]

Η μέθοδος void push(E e) είναι συνώνυμη της void addFirst(E e) και χρησιμοποιείται όταν χρησιμοποιούμε την Deque ως στοίβα (όπως και η boolean offerLast(E e) είναι συνώνυμη της boolean offer(E e)).

Προσπέλαση στοιχείων

Φυσικά υπάρχει η μέθοδος iterator() ενώ η Deque διαθέτει και την descendingIterator() όπου μπορούμε να προσπελάσουμε τη διπλή ουρά αντίστροφα.

Η διεπαφή Queue διαθέτει δυο μεθόδους που επιστρέφουν το πρώτο στοιχείο της χωρίς να το σβήνουν από την ουρά: E element() και E peek(). Η διαφορά τους είναι ότι η πρώτη εμφανίζει μια εξαίρεση (exception) αν η ουρά είναι άδεια, ενώ η δεύτερη απλά επιστρέφει null.

jshell> q.element()
$7 ==> 10

jshell> q.peek()
$8 ==> 10

jshell> Queue<Integer> qq = new LinkedList<>();
qq ==> []

jshell> qq.element()
|  java.util.NoSuchElementException thrown
|        at LinkedList.getFirst (LinkedList.java:248)
|        at LinkedList.element (LinkedList.java:667)
|        at (#10:1)

jshell> qq.peek()
$9 ==> null

Αντίστοιχα αν δουλεύετε με την Deque:

jshell> deque
deque ==> [10, 20, 30]

jshell> deque.peekFirst()			// επιστρέφει null αν η ουρά είναι άδεια
$10 ==> 10

jshell> deque.peekLast()			// επιστρέφει null αν η ουρά είναι άδεια
$11 ==> 30

jshell> deque.getFirst()			// εμφανίζει NoSuchElementException αν η ουρά είναι άδεια
$12 ==> 10

jshell> deque.getLast()				// εμφανίζει NoSuchElementException αν η ουρά είναι άδεια
$13 ==> 30

Διαγραφή στοιχείων

Οι μέθοδοι E remove() και E poll() εξάγουν το πρώτο στοιχείο της ουράς. Η διαφορά τους είναι ότι η πρώτη εμφανίζει μια εξαίρεση (NoSuchElementException) αν η ουρά είναι άδεια, ενώ η δεύτερη απλά επιστρέφει null.

jshell> q.remove();
$14 ==> 10

jshell> q
q ==> [20, 30]

jshell> q.poll();
$15 ==> 20

jshell> q
q ==> [30]

jshell> q.poll();
$16 ==> 30

jshell> q
q ==> []

jshell> q.poll();
$17 ==> null

jshell> q.remove();
|  java.util.NoSuchElementException thrown
|        at LinkedList.removeFirst (LinkedList.java:274)
|        at LinkedList.remove (LinkedList.java:689)
|        at (#22:1)

Αντίστοιχες μεθόδους έχει και η Deque:

jshell> deque
deque ==> [10, 20, 30]

jshell> deque.pollFirst()
$18 ==> 10

jshell> deque.pollLast()
$19 ==> 30

jshell> deque
deque ==> [20]

jshell> deque.removeFirst()
$20 ==> 20

jshell> deque.removeLast()
|  java.util.NoSuchElementException thrown
|        at ArrayDeque.removeLast (ArrayDeque.java:369)
|        at (#21:1)

Τέλος, η pop() είναι συνώνυμη της removeFirst() (όπως και οι getFirst() και removeFirst() είναι συνώνυμες των element() και remove() της Queue).

Αναζήτηση στοιχείων

Η δομή δεδομένων Ουρά δε συνίσταται για αναζήτηση στοιχείων.

Ταξινόμηση

Αν η σειρά με την οποία θέλουμε να προσπελάσουμε τα στοιχεία είναι σημαντική, τότε μπορούμε να χρησιμοποιήσουμε μια ουρά προτεραιότητας ή PriorityQueue. Η σειρά (ταξινόμηση) των στοιχείων βασίζεται είτε στη φυσική σειρά των στοιχείων (αν υλοποιούν τη διεπαφή Comparable), είτε τη σειρά που ορίζει ένας Comparator που παρέχεται στη μέθοδο κατασκευής της PriorityQueue.

PriorityQueue() // φυσική ταξινόμηση, αρχική χωρητικότητα (11)
PriorityQueue(Collection<? extends E> c) // φυσική ταξινόμηση, εκτός κι αν c είναι τύπου PriorityQueue ή 
 // SortedSet οπότε κληρονομεί τη σειρά ταξινόμησης της
PriorityQueue(int initialCapacity) // φυσική ταξινόμηση
PriorityQueue(int initialCapacity, Comparator<? super E> comparator) // η ταξινόμηση ορίζεται από τον Comparator
PriorityQueue(PriorityQueue<? extends E> c) // ταξινόμηση αυτή της c
PriorityQueue(SortedSet<? extends E> c) // ταξινόμηση αυτή της c

Έστω π.χ. ότι έχουμε μια κλάση Task:

class Task {
	private String description;
	private LocalDate dueDate;
	private Priority priority;
	// getters/setters
	// hashCode/equals
	// toString()
	...
}

enum Priority {HIGH, MEDIUM, LOW};

Αν θέλουμε να επεξεργαστούμε αυτά τα έργα με βάση την προτεραιότητά τους:

Comparator<Task> priorityComparator = new Comparator<Task>() {
	public int compare(Task t1, Task t2) {
		return t1.getPriority().compareTo(t2.getPriority());
	}
};

Queue<Task> priorityQueue = new PriorityQueue<>(20, priorityComparator);
priorityQueue.add(new Task("Doctor appointment", LocalDate.parse("2019-11-18"), Priority.MEDIUM));
priorityQueue.add(new Task("Birthday party", LocalDate.parse("2019-09-02"), Priority.HIGH));
priorityQueue.add(new Task("Book hotel", LocalDate.parse("2019-07-15"), Priority.MEDIUM));
...
Task nextTask = priorityQueue.poll();   // θα επιστρέψει το Task με Priority.HIGH

Αντιγραφή

Οι διάφοροι τύποι ουρών διαθέτουν copy constructors:

PriorityQueue(Collection<? extends E> c);
PriorityQueue(PriorityQueue<? extends E> c);
PriorityQueue(SortedSet<? extends E> c);

ArrayDeque(Collection<? extends E> c);

LinkedList(Collection<? extends E> c);

Συγχώνευση

Σαν άσκηση, γράψτε μια μέθοδο union() στο jshell που θα ενώνει τα στοιχεία δυο ουρών προτεραιότητας που περνάτε ως ορίσματα στη μέθοδο.

Διαχωρισμός

Σαν άσκηση, γράψτε μια μέθοδο split() στο jshell που θα διαχωρίζει ένα μια ουρά με ακέραια στοιχεία σε δυο νέες ουρές που το ένα θα αποθηκεύει τα ζυγά και η άλλη τα μονά στοιχεία της αρχικής ουράς.

Ισότητα

jshell> Queue<Integer> q1 = new ArrayDeque<>();
q1 ==> []

jshell>  Queue<Integer> q2 = new LinkedList<>();
q2 ==> []

jshell> q1
q1 ==> [10, 20, 30]

jshell> q2
q2 ==> [10, 20, 30]

jshell> q1.equals(q2); 
$1 ==> false

Σύγκριση των διαφόρων υλοποιήσεων της Queue

	offer	peek	poll	size
PriorityQueue	O(logn)	O(1)	O(logn)	O(1)
LinkedList	O(1)	O(1)	O(1)	O(1)
ArrayDeque	O(1)	O(1)	O(1)	O(1)

Πηγή: [Naftalin, Wadler (2006)]

Όπως είπαμε, καλύτερη απόδοση έχει η ArrayDeque.

Ασκήσεις

1) Στο μάθημα 3.2 είδαμε ότι υπάρχει η παρωχημένη (legacy) κλάση Stack. Υλοποιήστε τη δική σας πιο αποδοτική κλάση Stack χρησιμοποιώντας μια υλοποίηση της Deque.

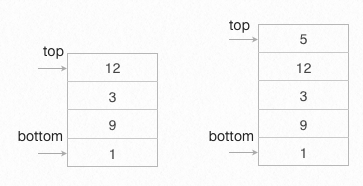
Εικόνα 3.5.4 Παράδειγμα στοίβας

Η διεπαφή της στοίβας είναι:

public class Stack<E> {
   	public boolean push(E e); // εισάγει ένα στοιχείο στο τέλος της στοίβας
	public E pop(); // εξάγει το τελευταίο στοιχείο που εισήχθηκε
	public E peek(); // επιστρέφει χωρίς να διαγράφει το τελευταίο στοιχείο που εισήχθηκε
	public boolean isEmpty(); // έλεγχος αν η στοίβα είναι κενή
	public boolena isFull(); // έλεγχος αν η στοίβα είναι γεμάτη
}

2) Μια συμβολοσειρά ονομάζεται παλινδρομική (palidrom) αν διαβάζεται το ίδιο και από τα δεξιά και από τ’ αριστερά (π.χ. η λέξη radar). Να γράψετε μια μέθοδο boolean palidrom(String s) που να διαβάζει μια συμβολοσειρά και να εξετάζει αν είναι παλιδρομική ή όχι. Υπόδειξη. Χρησιμοποιήστε τη δομή Στοίβα.

3) Για κάθε φυσικό αριθμό n>1, ο μικρότερος φυσικός d>1 διαιρεί το n καλείται πρώτος παράγοντας. Η παραγοντοποίηση του n με πρώτους παράγοντες βρίσκεται αν ο n αντικατασταθεί με το πηλίκο της διαίρεσης n/d μέχρις ότου n=1. Να γραφεί πρόγραμμα που να βρίσκει τους παράγοντες του n και να τους τυπώνει με φθίνουσα σειρά. Π.χ. για τον αριθμό 2100 να τυπώνει 7 5 5 3 2 2.

4) Να γραφεί μια μέθοδος boolean parenthesesOk(String s) που να διαβάζει ένα αλφαριθμητικό και να επιστρέφει true αν περιέχει ισοζυγισμένες παρενθέσεις, δηλ. για κάθε αριστερή παρένθεση (αν υπάρχει) να υπάρχει και η αντίστοιχή της δεξιά παρένθεση.

5) Στο τελευταίο βίντεο του μαθήματος είδαμε μια υλοποίηση της Q με χρήση της Deque. Δοκιμάστε την κλάση Q δημιουργώντας ένα νέο αντικείμενο της κλάσης μεγέθους 3 και προσθέστε τρία αντικείμενα σ’ αυτή. Τι συμβαίνει όταν γεμίσει η ουρά; Προσπαθήστε να προσθέσετε ακόμα ένα αντικείμενο. Ποια η συμπεριφορά της ουράς; Τι επιστρέφει η μέθοδος isFull(); Εξάγετε όλα τ’ αντικείμενα που εισάγατε και ακόμα ένα. Τι επιστρέφει η ουρά; Ελέγξτε τι επιστρέφει η isEmpty(). Τι θα συμβεί αν εισάγετε τιμή null στην ουρά;

6) Πώς θα μπορούσατε να ‘χακάρετε’ την κλάση Q; Π.χ. μπορείτε να δημιουργήσετε μια ουρά Q<Integer> που να γεμίσει τη μνήμη του υπολογιστή (να μη δουλέψει δηλ. η isFull()); Αφού βρείτε το bug, πώς μπορείτε να το διορθώσετε;

---

<-

Δ

->

---