2.3 Πίνακες ή Συστοιχίες (Arrays)

© Γιάννης Κωστάρας

---

<

Δ

>

---

Μαθησιακοί στόχοι

Σε αυτήν την ενότητα θα μάθουμε:

• τον τύπο δεδομένων πίνακας ή συστοιχία (array) μιας και πολλών διαστάσεων
• τρόπους αρχικοποίησης πινάκων
• τις βασικές λειτουργίες τους
• την κλάση Arrays

Εισαγωγή

Υποθέστε ότι σας έχουν αναθέσει την ανάπτυξη ενός προγράμματος Java που σκοπός του είναι η καταγραφή των υπαλλήλων της εταιρίας στην οποία δουλεύετε. Με τα όσα έχετε μάθει μέχρι τώρα, θα δημιουργούσατε τόσες διαφορετικές μεταβλητές όσες και οι υπάλληλοι της εταιρίας. Για μια μικρή εταιρία ίσως αυτό να είναι αποδεκτό, αλλά τι θα κάνατε αν δουλεύατε σε μια εταιρία 1000 ατόμων;

Ο πίνακας ή συστοιχία είναι η πιο απλή δομή δεδομένων (data structure). Αποθηκεύει ένα σύνολο στοιχείων του ίδιου τύπου δεδομένων. Τα στοιχεία του αποθηκεύονται σε συνεχόμενες θέσεις μνήμης ενώ η αναφορά σ’ ένα στοιχείο γίνεται μέσω δεικτών (indexes).

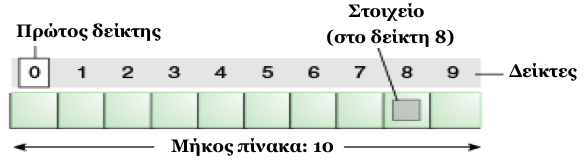
Εικόνα 2.3.1 Πίνακας ή συστοιχία (array)

Το 1ο στοιχείο αποθηκεύεται στη θέση 0:

Τύπος_δεδομένων όνομα_μεταβλητής[];

Π.χ. το παρακάτω τμήμα κώδικα δημιουργεί μια συστοιχία που μπορεί να αποθηκεύσει μέχρι 10 στοιχεία.

// Τ[] arrayname = new Τ[n];
jshell> int SIZE = 10;
SIZE ==> 10
jshell> int[] bathmoi = new int[SIZE];
bathmoi ==> int[10] { 0, 0, …, 0}

Τρόποι αρχικοποίησης πίνακα

jshell> int[] numbers = { 1, 2, 3 }
numbers ==> int[3] { 1, 2, 3 }
jshell> int[] numbers2 = new int[3]
numbers2 ==> int[3] { 0, 0, 0 }
jshell> String[] strings = new String[] { "a", "b", "c" };
strings ==> String[3] { "a", "b", "c" }
jshell> strings.length  
$1==> 3

Η εντολή length επιστρέφει το μέγεθος του πίνακα, όχι πόσα στοιχεία έχουν καταχωρηθεί σ’ αυτόν. Π.χ.

jshell> int[] array = new int[3]
array ==> int[3] { 0, 0, 0 } 
jshell> array[0]=10
$2 ==> 10
jshell> array.length
$3==> 3

Βασικές λειτουργίες

Ο πίνακας αποτελεί μια από τις πολλές δομές δεδομένων της γλώσσας Java. Θα εξετάσουμε αυτές τις δομές δεδομένων όσων αφορά τις ακόλουθες λειτουργίες:

Προσπέλαση	int b = bathmoi[1]; // 2ο στοιχείο
Εισαγωγή/εκχώρηση	bathmoi[5] = 18
Διαγραφή	(βλ. παρακάτω)
Αναζήτηση	int index = Arrays.binarySearch(bathmoi, key)
Ταξινόμηση	Arrays.sort(bathmoi)
Αντιγραφή	int[] b=Arrays.copyOfRange(bathmoi, 0, SIZE)
Συγχώνευση	(βλ. παρακάτω)
Διαχωρισμός	(βλ. παρακάτω)
Μήκος/Μέγεθος	bathmoi.length

Πολυδιάστατοι πίνακες

Ο ορισμός

// Τ[] arrayname = new Τ[n];

ορίζει έναν μονοδιάστατο πίνακα. Η έννοια του μονοδιάστατου πίνακα μπορεί να γενικευθεί και σε πίνακες περισσοτέρων διαστάσεων, π.χ. δισδιάστατων, τρισδιάστατων κ.ο.κ.

Π.χ. ένας δισδιάστατος πίνακας ορίζεται ως εξής:

// Τ[][] arrayname = new Τ[m][n];
jshell> int m = 2, n = 3;
m ==> 2
n ==> 3
jshell> int[][] matrix = new int[m][n];
matrix ==> int[2][] {int[3] {0, 0, 0}, int[3] {0, 0, 0}}

Τρόποι ορισμού δισδιάστατου πίνακα:

jshell> int[][] numbers = { { 1, 2, 3 }, { 4, 5, 6 } };
numbers ==> int[2][] { int[3] { 1, 2, 3 }, int[3] { 4, 5, 6 }}
jshell> int[][] numbers2 = new int[2][3];
numbers2 ==> int[2][] { int[3] { 0, 0, 0 }, int[3] { 0, 0, 0}}
jshell> int[][] a = { {1}, {2, 3}, null }; // πίνακας με γραμμές διαφόρων μεγεθών (ragged table)
a ==> int[3][] { int[1] { 1 }, int[2] { 2, 3 }, null }
jshell> a.length  // επιστρέφει τον αρ. των γραμμών του πίνακα
$3==> 3
jshell> a[0]
$4 ==> int[1] {1}
jshell> a[0].length
$5 ==> 1
jshell> numbers2[0][1] = 6
$6 ==> 6

1	2	3
4	5	6

Εικόνα 2.3.2 Εσωτερική αναπαράσταση δισδιάστατου πίνακα

Η κλάση Arrays

Η κλάση Arrays παρέχει χρήσιμες μεθόδους για τους πίνακες.

jshell> String[] strings = new String[3];
strings ==> String[3] { null, null, null }

jshell> import java.util.Arrays;

jshell> Arrays.fill(strings, "a");

jshell> strings
strings ==> String[3] { "a", "a", "a" }

jshell> Arrays.fill(strings, 1, 2, "b");

jshell> strings
strings ==> { "a", "b", "a" }

jshell> String[] strings_ = new String[3];
strings_ ==> String[3] { null, null, null }

jshell> Arrays.fill(strings_, "a");

jshell> strings_
strings_ ==> String[3] { "a", "a", "a" }

jshell> Arrays.mismatch(strings, strings_);
$1 ==> 1

Προτού τη χρησιμοποιήσουμε, θα πρέπει να εισάγουμε το αντίστοιχο πακέτο (package) java.util.Arrays. Η mismatch() είναι μια πολύ γρήγορη μέθοδος που προστέθηκε στην έκδοση 11 και μας επιτρέπει να συγκρίνουμε αν δυο συστοιχίες είναι ίσες (-1), διαφορετικά επιστρέφει τον πρώτο δείκτη όπου οι δυο συστοιχίες διαφέρουν.

Παρόμοια είναι και η Arrays.compare() η οποία συγκρίνει δυο συστοιχίες λεξικογραφικά. Μια αρνητική τιμή σημαίνει ότι η πρώτη συστοιχία είναι λεξικογραφικά πριν από την δεύτερη, μια θετική τιμή ότι η είναι μετά ενώ μηδενική τιμή σημαίνει ότι οι δυο συστοιχίες είναι ίσες. Ας δούμε ένα παράδειγμα για να το καταλάβουμε καλύτερα:

jshell> Arrays.compare(strings, strings_);
1

Αυτό σημαίνει ότι η strings είναι λεξικογραφικά μετά την strings_ επειδή το δεύτερο στοιχείο της (b) είναι λεξικογραφικά μετά το δεύτερο στοιχείο της strings_ (a).

Βασικές λειτουργίες πινάκων

Προσπέλαση στοιχείων πίνακα

jshell> int[] array = new int[10];
array ==> int[10] { 0, 0, 0, ..., 0 }
jshell> for (int i = 0; i < array.length; i++) {
          array[i] = i;
        }; 
jshell> array 
array ==> int[10] { 0, 1, 2, ... }
jshell> for (int e : array) {
           System.out.print(e + " ");
        }
0 1 2 3 4 5 6 7 8 9 

Σ’ αυτό το παράδειγμα βλέπουμε μια νέα σύνταξη της εντολής βρόγχου for που χρησιμοποιείται για να προσπελάζουμε πίνακες (αλλά και άλλες συλλογές όπως θα δούμε αργότερα).

Ας δούμε πως μπορούμε να προσπελάσουμε τα στοιχεία ενός δισδιάστατου πίνακα:

jshell> int[][] matrix = new int[5][5]; 
matrix ==> int[5][] { int[5] { 0, 0, 0, 0, 0 }, int[5] { 0,  ... int[5] { 0, 0, 0, 0, 0 } }
jshell> for (int i = 0; i < matrix.length; i++) {
           for (int j = 0; j < matrix[i].length; j++) {
              matrix[i][j] = i+j;
           }
        } 
jshell> for (int[] numbers : matrix) {
           for (int e : numbers) {
              System.out.print(e + " ");
           }
           System.out.println();    
        }
0 1 2 3 4 
1 2 3 4 5 
2 3 4 5 6 
3 4 5 6 7 
4 5 6 7 8 

Εκτύπωση πινάκων

jshell> int[] array = {1, 2, 3, 4, 5};
array ==> int[5] {1, 2, 3, 4, 5}
jshell> Arrays.toString(array);
$1 ==> "[1, 2, 3, 4, 5]"
jshell> int[][] array2d = {
{1, 2, 3},
{4, 5, 6},
{7, 8, 9}
};
array2d ==> int[3][] { int[3] { 1, 2, 3 }, int[3] { 4, 5, 6 }, int[3] { 7, 8, 9 } }
jshell> Arrays.deepToString(array2d)
$2 ==> "[[1, 2, 3], [4, 5, 6], [7, 8, 9]]"

Ταξινόμηση πινάκων

jshell> int[] array = {2, 9, -1, 4, 13};
$3 ==> int[5] {2, 9, -1, 4, 13}

jshell> Arrays.sort(array); // με αριθμητική σειρά

jshell> Arrays.toString(array);
$4 ==> "[-1, 2, 4, 9, 13]"

jshell> Arrays.sort(array, 0, array.length, Collections.reverseOrder()); // με αντίστροφη αριθμητική σειρά
|  Error:
|  no suitable method found for sort(int[],int,int,java.util.Comparator<java.lang.Object>)
|      method java.util.Arrays.<T>sort(T[],java.util.Comparator<? super T>) is not applicable
|        (cannot infer type-variable(s) T
|          (actual and formal argument lists differ in length))
|      method java.util.Arrays.<T>sort(T[],int,int,java.util.Comparator<? super T>) is not applicable
|        (inference variable T has incompatible bounds
|          equality constraints: int
|          lower bounds: java.lang.Object)
|  Arrays.sort(array, 0, array.length, Collections.reverseOrder());
|  ^---------^

jshell> String[] names = {"Κώστας", "Γιάννης", "Κατερίνα", "Μαρία", "Ανάργυρος"};
names ==> String[5] { "Κώστας", "Γιάννης", "Κατερίνα", "Μαρία", "Ανάργυρος" }

jshell> Arrays.sort(names, 0, names.length, Collections.reverseOrder()); // λεξικογραφικά
// "["Μαρία", "Κώστας", "Κατερίνα", "Γιάννης", "Ανάργυρος"]"

Παρατηρήστε ότι δουλεύει μόνο σε αντικείμενα κλάσεων (όπως η String[]) και όχι σε πρωτογενής τύπους (π.χ. int[]).

Αναζήτηση στοιχείων σε πίνακα

jshell> int[] array = {1, 2, 3, 4, 5};
array ==> int[5] {1, 2, 3, 4, 5}
jshell> Arrays.binarySearch(array, 4); // εύρεση του 4
$5 ==> 3  // επιστρέφει τον δείκτη αν βρέθηκε, ή έναν αρνητικό αριθμό (-(insertion point) - 1) αν δε βρέθηκε 

Ο αλγόριθμος δυαδικής αναζήτησης (BinarySearch) βρίσκει ένα στοιχείο σε μία ταξινομημένη λίστα ψάχνοντας κάθε φορά στη μέση του πίνακα. Αν το στοιχείο είναι μεγαλύτερο τότε ο πίνακας μοιράζεται στη μέση και ο αλγόριθμος επαναλαμβάνεται μόνο στο δεξί τμήμα του πίνακα έως ότου βρεθεί το στοιχείο.

Αντιγραφή πινάκων

jshell> int[] newArray = Arrays.copyOf(array, array.length+1); // δημιουργία ενός newArray μήκους array.length+1 με τα στοιχεία του array
newArray ==> int[6] { 1, 2, 3, 4, 5, 0 }
jshell> int[] newArray = Arrays.copyOfRange(array, 1, 2); // αντιγραφή μέρους του αρχικού πίνακα
newArray ==> int[1] { 2 }
jshell> int[] clonedArray = array.clone()
clonedArray ==> int[5] { 1, 2, 3, 4, 5 }

ή

System.arraycopy( <source table>, <source start index>, 
            <dest table>, <dest start index>, <dest end index>);

π.χ.

jshell> int[] array2 = new int[5]
array2 ==> int[5] { 0, 0, 0, 0, 0 }

jshell> System.arraycopy(array, 0, array2, 0, 5);

jshell> array2
array2 ==> int[5] { 1, 2, 3, 4, 5 }

Διαγραφή στοιχείων πινάκων

jshell> int[] array = {1, 2, 3, 4, 5};
array ==> int[5] {1, 2, 3, 4, 5}
// Πώς μπορούμε να διαγράψουμε ένα στοιχείο;
jshell> int[] newArray = new int[array.length-1]
newArray ==> int[4] {0, 0, 0, 0}
jshell> int index = 1; // θέλουμε να διαγράψουμε το 2ο στοιχείο
jshell> System.arraycopy(array, 0, newArray, 0, index);
// αντιγραφή από το 0 μέχρι το array[index-1]
jshell> newArray
newArray ==> int[4] { 1, 0, 0, 0 }
jshell> System.arraycopy(array, index + 1, newArray, index, array.length - index - 1); // αντιγραφή από array[index+1] μέχρι array[array.length-1]
jshell> newArray
newArray ==> int[4] { 1, 3, 4, 5 }

Ισότητα πινάκων

jshell> Arrays.equals(array, newArray); 
$1 ==> false
jshell> Arrays.deepEquals(array2d, newArray2d); // για n-διαστάσεις
$1 ==> false

Κατηγορίες δισδιάστατων πινάκων

• Τετραγωνικός λέγεται ο δισδιάστατος πίνακας του οποίου το μέγεθος των δυο διαστάσεων είναι ίσο (δηλ. m=n)
• Συμμετρικός λέγεται ένας τετραγωνικός πίνακας με στοιχεία a[i][j]=a[j][i] για 0<=i,j<=n-1. Π.χ.

1	6	7	9
6	2	5	8
7	5	3	0
9	8	0	4

• Τριγωνικοί ονομάζονται οι τετραγωνικοί πίνακες που έχουν μηδενικά στοιχεία από τη μια μεριά της διαγωνίου. Διακρίνονται σε άνω τριγωνικούς (a[i][j] = 0 αν i>j) και κάτω τριγωνικούς (a[i][j] = 0 αν i<j). Αν τα στοιχεία της διαγωνίου είναι επίσης μηδέν, τότε ο πίνακας λέγεται αυστηρά πάνω (κάτω) τριγωνικός. Τέλος, η γενίκευση των τριγωνικών πινάκων σε ανώτερες διαστάσεις, ονομάζεται τετραεδικός πίνακας. Π.χ. ένας κάτω τριγωνικός πίνακας

1	0	0	0
6	2	0	0
7	5	3	0
9	8	0	4

• Ένας τριδιαγώνιος πίνακας είναι ένας τετραγωνικός πίνακας με μηδενικά όλα τα στοιχεία εκτός από τα στοιχεία της κύριας διαγωνίου και των δυο διπλανών προς την κύρια διαγώνιο. Π.χ.

1	6	0	0
6	2	9	0
0	5	3	8
0	0	9	4

Συγχώνευση πινάκων

Μπορούμε να συγχωνεύσουμε δυο ή περισσότερους πίνακες για να δημιουργήσουμε έναν άλλο πίνακα. Το ερώτημα είναι τι πράξη κάνουμε κατά τη συγχώνευση. Αυτό εξαρτάται κάθε φορά από το πρόβλημά μας.

Ας δούμε μερικά παραδείγματα. Από τα μαθηματικά έχουμε μάθει για τις πράξεις πινάκων.

Πρόσθεση πινάκων

1	2	3		4	5	6		5	7	9
4	5	6	+	7	8	9	=	11	13	15
7	8	9		1	2	3		8	10	12

int[][] a = { { 1, 2, 3 }, { 4, 5, 6 }, { 7, 8, 9 } };
int[][] b = { { 4, 5, 6 }, { 7, 8, 9 }, { 1, 2, 3 } };
int[][] c = new int[3][3];
for (int i=0; i<3; i++) {
    for (int j=0; j<3; j++) {
      c[i][j] = a[i][j] + b[i][j];
    }
}

Πολλαπλασιασμός πινάκων

1	2	3		4	5		21	27
4	5	6	*	7	8	=	57	72
1	2

c[0][0] = a[0][0]*b[0][0] + a[0][1]*b[1][0] + a[0][2]*b[2][0]: 1 * 4 + 2 * 7 + 3 * 1 = 21
c[0][1] = a[0][0]*b[0][1] + a[0][1]*b[1][1] + a[0][2]*b[2][1]: 1 * 5 + 2 * 8 + 3 * 2 = 27
c[1][0] = a[1][0]*b[0][0] + a[1][1]*b[1][0] + a[1][2]*b[2][0]: 4 * 4 + 5 * 7 + 6 * 1 = 57
c[1][1] = a[1][0]*b[0][1] + a[1][1]*b[1][1] + a[1][2]*b[2][1]: 4 * 5 + 5 * 8 + 6 * 2 = 72

Online εργαλείο πολλ/σμού πινάκων

int[][] a = { { 1, 2, 3 }, { 4, 5, 6 } };
int[][] b = { { 4, 5 }, { 7, 8 }, { 1, 2 } };
int[][] c = new int[a.length][b[0].length];
for (int row=0; row < a.length; row++) {
    for (int col=0; col < b[row].length; col++) {
        for (int i = 0; i < b.length; i++) {
            c[row][col] += a[row][i] * b[i][col];
          }
    }
}
for (int i=0; i < c.length; i++) {
    for (int j=0; j < c[i].length; j++) {
        System.out.print(" | " + c[i][j]);
    }
    System.out.println(" |");
}

 | 21 | 27 |
 | 57 | 72 |

Διαχωρισμός πινάκων

Π.χ. δοθέντος ενός πίνακα ακεραίων, δημιουργήστε δυο πίνακες που θα περιέχουν ο ένας τους θετικούς και ο άλλος τους αρνητικούς αριθμούς του πίνακα.

Έστω:

int[] a = {5, -7, 0, -1, 3, 12};
int[] p = new int[a.length];  // μπορεί όλα τα στοιχεία να 'ναι θετικοί ή μηδέν
int[] n = new int[a.length];  // μπορεί όλα τα στοιχεία να 'ναι αρνητικοί
int pi = 0, ni = 0;
for (int e : a) {
  if (e >= 0) {
    p[pi++] = e;
  } else {
    n[ni++] = e;
  }
}
for (int i=0; i < pi; i++) {
  System.out.print(" " + p[i]);
}
System.out.println();
for (int i=0; i < ni; i++) {
  System.out.print(" " + n[i]);
}

 5 0 3 12
 -7 -1

Μπορείτε να πειραματιστείτε περαιτέρω εδώ .

Εφαρμογές

Ας ξεκινήσουμε με μια σχετικά απλή άσκηση, να αντιμεταθέσουμε τα στοιχεία ενός πίνακα.

jshell> int[] array = {1, 2, 3, 4, 5};
$1 ==> int[5] {5, 4, 3, 2, 1}

Ας δούμε βήμα-βήμα τι θέλουμε να επιτύχουμε. Θέλουμε να αλλάξουμε τη θέση του 1 με το 5. Θα χρειαστούμε δυο δείκτες, έναν που να δείχνει στο 1 (έστω i) κι έναν που να δείχνει στην τελευταία θέση του πίνακα (έστω j). Αφού αντιμεταθέσουμε το στοιχείο που δείχνει ο i με το στοιχείο που δείχνει ο j, θα πρέπει να προσαυξήσουμε τον i κατά ένα και να μειώσουμε τον j κατά ένα και να επαναλάβουμετη διαδικασία μέχρις ότου i == j. Ας μετατρέψουμε τον παραπάνω αλγόριθμο σε κώδικα:

int i = 0;
int j = array.length - 1;
while (i < j) {
   //αντιμετάθεσε τα στοιχεία στις θέσεις i και j
   int temp = array[i];
   array[i] = array[j];
   array[j] = temp;
   i++;
   j--;
}
Arrays.toString(array);
// [5, 4, 3, 2, 1]

Πώς μπορούμε να βρούμε το μέγιστο στοιχείο ενός μη ταξινομημένου πίνακα;

int[] array = {2, 9, -1, 4, 13};
int max = Integer.MIN_VALUE;   // φρουρός (sentinel), μια τιμή που δεν είναι έγκυρη για το πρόβλημά μας
for (int i = 0; i < array.length; i++) {
    if (array[i] > max) {
        max = array[i];
    }
}
System.out.println("Το μεγαλύτερο στοιχείο του πίνακα είναι: " + max);

Τροποποιήστε το παραπάνω πρόγραμμα ώστε να βρείτε το ελάχιστο στοιχείο του πίνακα.

Οι πιο συνήθεις εφαρμογές των πινάκων είναι αυτές της αναζήτησης στοιχείων και της ταξινόμησής τους. Αν και είδαμε πιο πάνω ότι η κλάση Arrays διαθέτει κατάλληλες μεθόδους για το σκοπό αυτό (sort(), binarySearch()) υπάρχουν πολλοί αλγόριθμοι που καλό είναι να τους γνωρίζετε.

Ας υποθέσουμε ότι έχουμε τον παρακάτω πίνακα ακέραιων στοιχείων:

jshell> int[] array = {2, 9, -1, 4, 13};
$1 ==> int[5] {2, 9, -1, 4, 13}

Ένας από τους απλούστερους αλγόριθμους αναζήτησης είναι η γραμμική αναζήτηση (linear search). Σ’ αυτήν αναζητούμε ένα στοιχείο από την αρχή του πίνακα. Αν ο πίνακας έχει n στοιχεία, τότε στη χειρότερη περίπτωση ο αλγόριθμος αυτός θα χρειαστεί να αναζητήσει όλα τα στοιχεία του πίνακα (λέμε ότι έχει απόδοση O(n)).

Ας υποθέσουμε ότι αναζητούμε αν το 4 υπάρχει στην παραπάνω συστοιχία. Θα χρειαστούμε ένα δείκτη (i) για να προσπελάσουμε τα στοιχεία της συστοιχίας από την αρχή της και άλλη μια μεταβλητή pos που θα μας δείξει τη θέση στην οποία βρίσκεται το στοιχείο και η οποία αρχικοποιείται με την τιμή -1. Στη συνέχεια προσπελάζουμε ένα ένα τα στοιχεία της συστοιχίας και τα συγκρίνουμε με το στοιχείο που αναζητούμε. Αν το βρήκαμε, τότε θέτουμε την pos = i και σταματάμε το βρόγχο, αλλιώς αυξάνουμε την i και συνεχίζουμε στο επόμενο στοιχείο της συστοιχίας.

int search = 4;
int pos = -1;
int i = 0;
while (i < array.length && pos == -1) {
   if (array[i] == search) {
      pos = i;
   } else {
      i++;
   }
}
if (pos > -1) { 
    System.out.println("Βρέθηκε στη θέση: " + pos); // Βρέθηκε στη θέση: 3
} else { 
    System.out.println("Δεν βρέθηκε"); 
}

Ο αλγόριθμος γραμμικής αναζήτησης δουλεύει τόσο με ταξινομημένους όσο και με αταξινόμητους πίνακες και αποτελεί απάντηση στην άσκηση 2.

Ο αλγόριθμος γραμμικής αναζήτησης δεν είναι τόσο αποτελεσματικός για συστοιχίες με πάρα πολλά στοιχεία. Γι’ αυτό το λόγο έχουν αναπτυχθεί άλλοι αλγόριθμοι αναζήτησης. Ένας απ’ αυτούς είναι ο αλγόριθμος δυαδικής αναζήτησης (binary search) τον οποίο υλοποιεί η Arrays.binarySearch().

Ο αλγόριθμος δυαδικής αναζήτησης περιγράφεται εδώ ενώ μια αναπαράστασή του μπορείτε να δείτε στο φωτόδεντρο. Το μειονέκτημά του είναι ότι δουλεύει μόνο με ταξινομημένους πίνακες. Χωρίζει τον πίνακα σε δυο υποπίνακες και ελέγχει αν το στοιχείο που ψάχνει είναι στον αριστερό ή τον δεξί υποπίνακα, τον οποίο με τη σειρά του χωρίζει πάλι σε δυο υποπίνακες κ.ο.κ.

Έστω ότι έχουμε τον ακόλουθο ταξινομημένο πίνακα:

jshell> int[] array = {0,7,14,16,17,25,29,30,40,41,44,45,47,57,58};
array ==> int[15] { 0, 7, 14, 16, 17, 25, 29, 30, 40, 41, 44, 45, 47, 57, 58 }

και ας προσπαθήσουμε να υλοποιήσουμε σε Java τον αλγόριθμο που περιγράφεται στο Φωτόδεντρο. Θα χρειαστούμε δυο μεταβλητές που να δηλώνουν την αρχή και το τέλος του υποπίνακα και έστω ότι αναζητούμε το 40. Υπολογίζουμε τον δείκτη (middle) που δείχνει στο μέσο του πίνακα. Αν το στοιχείο που ψάχνουμε είναι μικρότερο από το μεσαίο στοιχείο του πίνακα, τότε αυτό σημαίνει ότι βρίσκεται στο αριστερό υποπίνακα που αποτελείται από το στοιχείο που δείχνει ο start και ένα στοιχείο πριν από τον middle ενώ αν είναι μεγαλύτερο από το μεσαίο στοιχείο του πίνακα, τότε αυτό θα βρίσκεται σε μια θέση μετά από τον middle μέχρι εκεί που δείχνει ο end.

int start = 0, end = array.length-1;
int search = 40;
boolean found = false;
boolean found = false;
while (start <= end && !found) {
  int middle = (start + end) / 2;
  if (array[middle] < search) {
    start = middle + 1;
  } else if (array[middle] > search) {
    end = middle - 1;
  } else if (array[middle] == search) {
    found = true;
  } 
}
System.out.println("Βρέθηκε;" + found);

Ο παραπάνω αλγόριθμος έχει bug. Το bug, το οποίο βρέθηκε το 2006, είχε και η υλοποίηση της Arrays.binarySearch(). Το λάθος βρίσκεται σ’ αυτή τη γραμμή:

int middle =(start + end) / 2;

Όπως περιγράφεται στο άρθρο, ο αλγόριθμος αποτυγχάνει αν start + end > Integer.MAX_VALUE. Η παραπάνω γραμμή θα πρέπει να αντικατασταθεί με:

int middle = start + ((end - start) / 2);

Σαν έξτρα άσκηση, τροποποιήστε το παραπάνω πρόγραμμα ώστε να εμφανίζει και την θέση στην οποία βρέθηκε ο αριθμός, ή -1 αν δεν βρέθηκε.

Ας επιλύσουμε την άσκηση 3. Ο αλγόριθμος αυτός ψάχνει το μικρότερο στοιχείο του πίνακα και το αντιμεταθέτει με την τρέχουσα θέση του δείκτη. Στη συνέχεια αυξάνει το δείκτη κατά ένα και επαναλαμβάνει τη διαδικασία. Το αποτέλεσμα είναι ένας ταξινομημένος πίνακας. Π.χ. δείτε το βίντεο.

int[] array = {2, 9, -1, 4, 1};
for (int i=0; i< array.length; i++) {
  System.out.print(" " + array[i]);
}
// 2 9 -1 4 1
for (int i = 0; i < array.length - 1; i++) {
    int min = i;
    for (int j = i+1; j < array.length; j++) {
        if (array[min] > array[j]) {
            min = j;    // εύρεση του δείκτη που 'χει το μικρότερο στοιχείο του πίνακα από το i και μετά
        }
    }
    // αντιμετάθεση του στοιχείου array[i] με το array[min]
    int temp = array[min];
    array[min] = array[i];
    array[i] = temp;
}
System.out.println();
Arrays.toString(array);
// -1 1 2 4 9

Άλλοι γνωστοί αλγόριθμοι ταξινόμησης είναι ο αλγόριθμος φυσσαλίδας (bubble sort) και ο αλγόριθμος γρήγορης ταξινόμησης (quick sort).

Π.χ. η μέθοδος της φυσσαλίδας δουλεύει ως εξής. Αν περιστρέψουμε έναν πίνακα n στοιχείων κατά 90° (ώστε το τελευταίο στοιχείο του να ‘ναι κάτω), τότε:

1. Σύγκρινε ζευγάρια διαδοχικών στοιχείων, από κάτω προς τα επάνω, και όταν βρίσκεις δύο που δεν είναι στη σωστή σειρά, αντιμετάθεσέ τα. Μετά από το πρώτο πέρασμα, πρώτο στοιχείο θα είναι το μικρότερο όλων.
2. Κάνε και δεύτερο πέρασμα, για τα στοιχεία από το δεύτερο και μετά, οπότε έτσι θα έλθει και το δεύτερο κατά σειρά στη θέση του.
3. Μετά από n−1 περάσματα συνολικά, ο πίνακας θα έχει ταξινομηθεί.

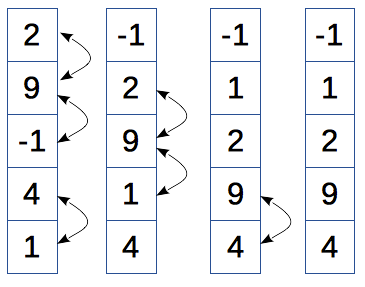
jshell> int[] array = {2, 9, -1, 4, 1};
array ==> int[5] { 2, 9, -1, 4, 1 }

jshell> for (int i = 0; i < array.length - 1; i++) {
   ...>     for (int j = array.length - 1; j > i; j--) {
   ...>         if (array[j-1] > array[j]) {
   ...>             // αντιμετάθεση του στοιχείου array[j-1] με το array[j]
   ...>             int temp = array[j-1];
   ...>             array[j-1] = array[j];
   ...>             array[j] = temp;
   ...>         }
   ...>     }
   ...> }

jshell> array
array ==> int[5] { -1, 1, 2, 4, 9 }

Εικόνα 2.3.3 Σωρός (heap)

Ασκήσεις

1. Η δυαδική αναζήτηση απαιτεί τα στοιχεία του πίνακα να είναι ταξινομημένα. Πώς θα μπορούσατε να υλοποιήσετε τον αλγόριθμο χωρίς τη χρήση της Arrays.binarySearch();
2. Η δυαδική αναζήτηση απαιτεί τα στοιχεία του πίνακα να είναι ταξινομημένα. Γράψτε έναν αλγόριθμο αναζήτησης που δουλεύει τόσο σε ταξινομημένους όσο και σε αταξινόμητους πίνακες.
3. Ο αλγόριθμος ταξινόμησης με επιλογή (selection sort) ταξινομεί έναν πίνακα ως εξής: σε κάθε βήμα i βρίσκει το i-οστό πιο μικρό στοιχείο και το τοποθετεί στην θέση i. Υλοποιήστε αυτόν τον αλγόριθμο.
4. Για κάθε ένα από τα παρακάτω είδη πινάκων να γραφεί πρόγραμμα Java το οποίο θα διαβάζει έναν τετραγωνικό πίνακα ΝxΝ και θα εμφανίζει τι τύπου είναι ο πίνακας ή τίποτα από τα παρακάτω:
   • Συμμετρικός
   • Τριγωνικός
   • Τριδιαγώνιος
5. Πόσα 8-άρια υπάρχουν στους αριθμούς από το 1 μέχρι το 1 εκατομμύριο;
6. Να γράψετε ένα πρόγραμμα που να κατασκευάζει ένα μαγικό τετράγωνο 5x5, δηλ. ένα δισδιάστατο πίνακα με τους αριθμούς 1 έως 25, μία ϕορά ο καθένας, έτσι ώστε σε κάθε γραμμή, κάθε στήλη και κάθε μία από τις δύο διαγωνίους να έχουμε το ίδιο άθροισμα.

Πηγές

1. Horstmann C., Big Java 5 - Chapter 7 - Arrays and Array Lists

---

<

Δ

>

---